Understanding the Pythagoras theorem can be a tricky task for many students. But don’t worry! With the help of “Maths Genie Pythagoras,” you can easily master this essential concept. Whether you are a beginner or have already learned about it, this guide will walk you through the theorem, how to use it in real life, and how the Maths Genie can provide you with simple and clear answers.
In this post, we will break down the Pythagoras theorem in an easy-to-understand way and show you how to use Maths Genie Pythagoras to find answers to questions. By the end, you will have a stronger grasp of the Pythagorean theorem and feel confident solving problems on your own.
What is the Pythagoras Theorem?
Before we dive into Maths Genie Pythagoras answers, let’s first understand what the Pythagoras theorem is.
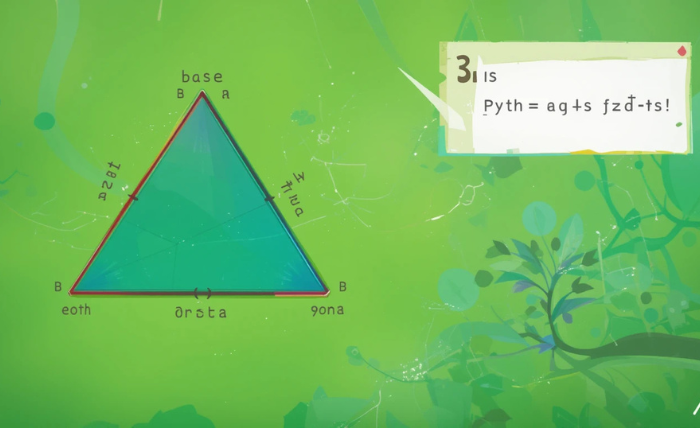
The Pythagorean theorem is a simple rule used in geometry, particularly when working with right-angled triangles. It states that in any right-angled triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. In simpler terms:
Hypotenuse2=Base2+Height2\text{Hypotenuse}^2 = \text{Base}^2 + \text{Height}^2Hypotenuse2=Base2+Height2
This formula is one of the most useful tools in geometry, helping us to calculate unknown sides of right-angled triangles.
How to Use the Pythagoras Theorem
Let’s look at how we can use the Pythagoras theorem in different problems. When you are given two sides of a right-angled triangle, you can use the Pythagorean theorem to calculate the third side.
Example 1: Finding the Hypotenuse
Suppose we have a triangle where the base is 3 cm and the height is 4 cm. We want to find the length of the hypotenuse.
Using the formula:
Hypotenuse2=Base2+Height2\text{Hypotenuse}^2 = \text{Base}^2 + \text{Height}^2Hypotenuse2=Base2+Height2
We plug in the numbers:
Hypotenuse2=32+42=9+16=25\text{Hypotenuse}^2 = 3^2 + 4^2 = 9 + 16 = 25Hypotenuse2=32+42=9+16=25
Now, we take the square root of 25 to find the length of the hypotenuse:
Hypotenuse=25=5 cm\text{Hypotenuse} = \sqrt{25} = 5 \text{ cm}Hypotenuse=25=5 cm
So, the hypotenuse is 5 cm.
Example 2: Finding a Missing Side
Now let’s say we know the hypotenuse and one side, and we need to find the other side. Suppose the hypotenuse is 10 cm, and the base is 6 cm. We can use the same formula but rearrange it to find the missing side:
Base2=Hypotenuse2−Height2\text{Base}^2 = \text{Hypotenuse}^2 – \text{Height}^2Base2=Hypotenuse2−Height2
So:
Base2=102−62=100−36=64\text{Base}^2 = 10^2 – 6^2 = 100 – 36 = 64Base2=102−62=100−36=64
Now, take the square root of 64:
Base=64=8 cm\text{Base} = \sqrt{64} = 8 \text{ cm}Base=64=8 cm
Therefore, the base of the triangle is 8 cm.
How Maths Genie Helps You Solve Pythagoras Problems
Maths Genie is an excellent resource for learning and solving problems related to the Pythagoras theorem. The platform provides clear explanations, helpful examples, and step-by-step solutions for all kinds of geometry problems.
Maths Genie Pythagoras Theorem
With Maths Genie Pythagoras, you can access detailed answers to various problems, from basic exercises to more complex ones. The website breaks down each problem into simple steps, making it easier for you to follow along. This makes learning the Pythagorean theorem both fun and educational.
Maths Genie Pythagoras Answers
If you get stuck while solving a problem, Maths Genie Pythagoras answers can be a lifesaver. The site provides worked-out solutions to problems, so you can see how the answer is reached. By studying these answers, you’ll improve your understanding and become more confident in your ability to solve similar problems.
Why Is the Pythagoras Theorem Important?
The Pythagoras theorem is not just a theoretical concept—it has practical uses in real life. Architects, engineers, and even video game designers use the Pythagorean theorem to calculate distances, angles, and dimensions in their work.
For example, if you want to measure the distance between two points on a map or build a ramp with a specific height and base, you can use the Pythagoras theorem to find the hypotenuse, which represents the distance or length you need.
Understanding the Pythagoras theorem is also essential for more advanced mathematical concepts, such as trigonometry, vector analysis, and even in fields like physics and computer science.
Maths Genie Pythagoras Theorem – Step-by-Step Process
Now, let’s explore how to solve Pythagoras problems with the help of Maths Genie Pythagoras theorem resources. Here’s a step-by-step guide to help you follow along:

Step 1: Identify the Right-Angled Triangle
Make sure the triangle you are working with has a right angle (90 degrees). If the triangle is not a right-angled triangle, you cannot apply the Pythagorean theorem.
Step 2: Label the Sides
Label the three sides of the triangle. The two shorter sides are usually called the “base” and “height.” The longest side, opposite the right angle, is called the “hypotenuse.”
Step 3: Apply the Pythagorean Theorem Formula
Now, use the formula:
Hypotenuse2=Base2+Height2\text{Hypotenuse}^2 = \text{Base}^2 + \text{Height}^2Hypotenuse2=Base2+Height2
Or, if you need to find one of the shorter sides:
Base2=Hypotenuse2−Height2\text{Base}^2 = \text{Hypotenuse}^2 – \text{Height}^2Base2=Hypotenuse2−Height2
Step 4: Solve the Equation
After applying the formula, simplify the equation to find the unknown side. You may need to use a calculator to square the numbers and then take the square root to get the final answer.
Step 5: Check Your Work
Once you have an answer, double-check it to ensure that the numbers make sense and that the triangle’s sides fit the formula.
Using Maths Genie Pythagoras Theorem Practice Questions
Maths Genie also provides practice questions for you to test your understanding of the Pythagoras theorem. These questions range from basic to advanced levels, so you can practice and build your confidence. After each question, Maths Genie Pythagoras theorem answers are available to show you the correct solution and help you learn from any mistakes.
Advanced Applications of the Pythagorean Theorem
As you continue learning, you’ll find that the Pythagorean theorem has more advanced applications. These include:
- 3D Geometry: The Pythagorean theorem can be applied to three-dimensional space, helping to calculate the distance between points in space or the length of diagonals in three-dimensional shapes.
- Trigonometry: The Pythagorean theorem is foundational for trigonometry, which deals with the relationships between the angles and sides of triangles.
- Real-Life Problems: As mentioned earlier, the Pythagoras theorem helps in real-life situations such as construction, navigation, and even sports.
Conclusion: Master the Pythagoras Theorem with Maths Genie
Learning the Pythagorean theorem doesn’t have to be difficult. With the help of Maths Genie Pythagoras answers, you can break down complex problems into simple steps and solve them with confidence. By practicing with Maths Genie, you will gradually gain the skills needed to master the Pythagorean theorem and apply it to various situations, both in school and beyond.
With consistent practice and guidance from Maths Genie Pythagoras, you will soon find yourself solving Pythagoras problems like a pro. So don’t hesitate—start practicing today, and remember, the more you practice, the better you’ll become!